Graph 3D - C++
This program implements my simple Vector3D.h source to draw simple graphs using SDL.
While it's not terribly advanced, it should be pretty fun to tinker with.
To learn more about 3D rotations including the mathematics and more source (Java) examples, view my previous post: 3D Rotation Matrix - Graph3D.
If you don't want the Graph utility, the single Vector3D C++ source file can be found here.
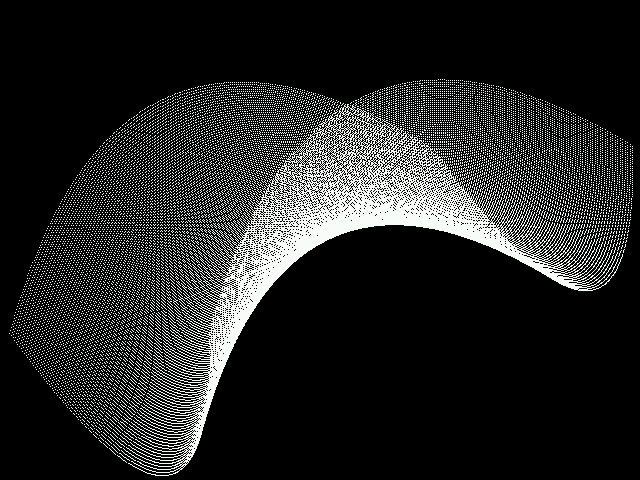
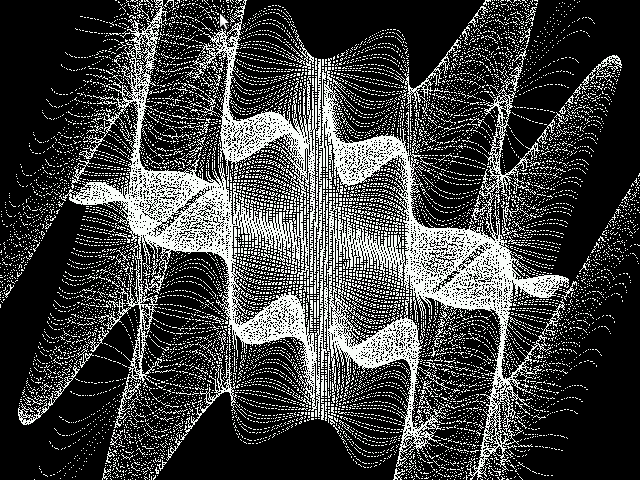
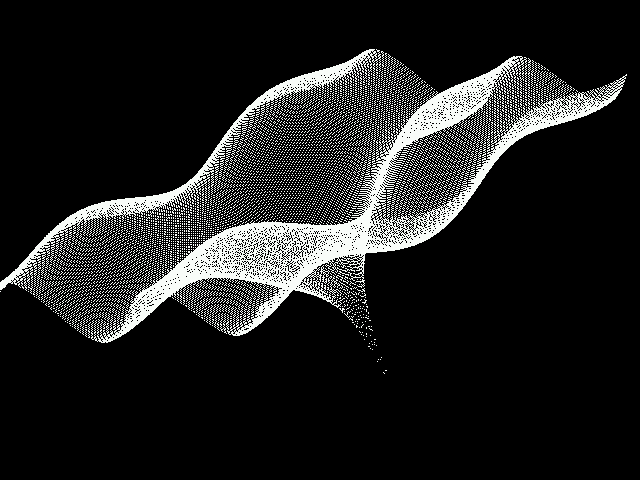
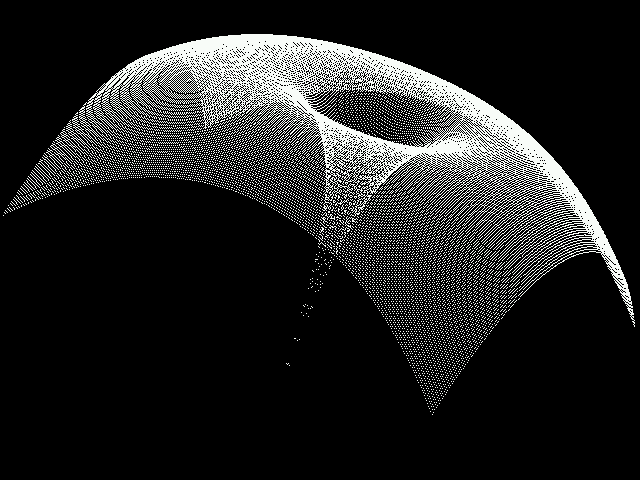
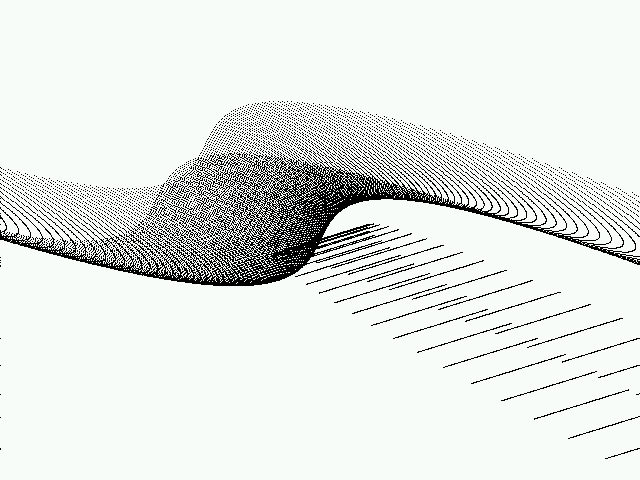
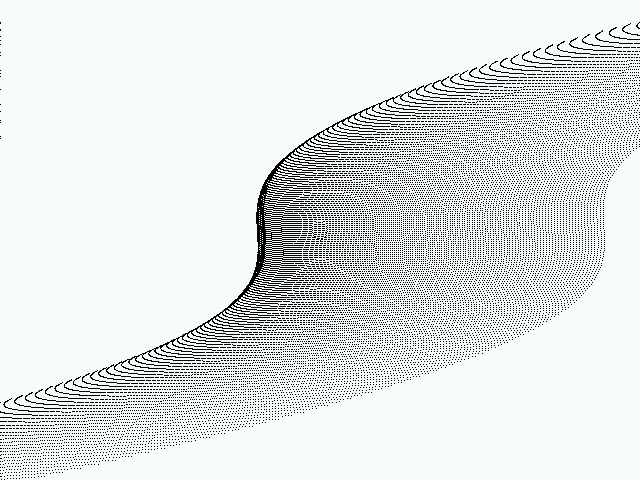
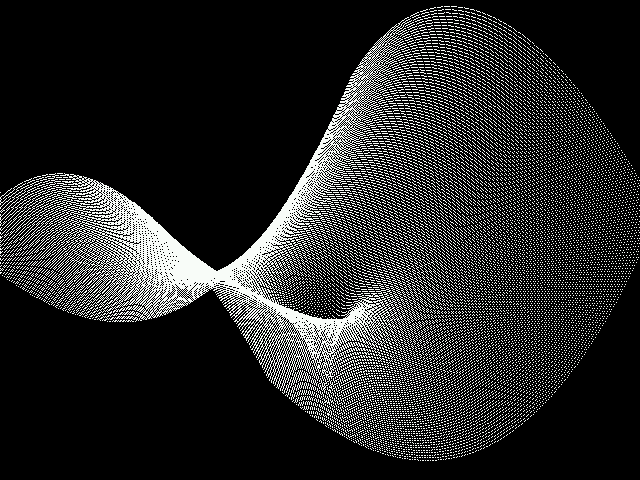
Below are a few of the graphs that I created. You may uncomment the function that you want to graph.
3D Function Plots
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Code
main.cpp
#include <iostream>
#include <cstdlib>
#include <SDL/SDL.h>
#include "Vector3D.h"
/*
3D Vector and rotation functions. Rotations about X, Y, Z, and any arbitruary Vector
*/
using namespace std;
void setPixel(SDL_Surface* surface, int x, int y, Uint32 pixel);
static double sigmoid(double x);
void keyboard();
void handleInput();
bool KEYS[322]; // 322 is the number of SDLK_DOWN events
// DEFAULTS
int xMax = 250;
int yMax = 250;
int pointsX = 400;
int pointsY = 400;
Vector3D** fx;
double xaxis = 320;
double yaxis = 240;
double rotSpeed = 0.1;
double thetaX = 0;
double thetaY = 0;
double thetaZ = 0;
int main ( int argc, char** argv ) {
// initialize SDL video
if ( SDL_Init( SDL_INIT_VIDEO ) < 0 ) {
cout << "Unable to init SDL: %s\n" << SDL_GetError() << endl;
return 1;
}
// make sure SDL cleans up before exit
atexit(SDL_Quit);
// create a new window
SDL_Surface* screen = SDL_SetVideoMode(640, 480, 16,
SDL_HWSURFACE|SDL_DOUBLEBUF);
if (!screen) {
cout << "Unable to set 640x480 video: %s\n" << SDL_GetError() << endl;
return 1;
}
for(int i = 0; i < 322; i++ ) {
KEYS[i] = false;
}
xMax = 250;
yMax = 250;
pointsX = 250;
pointsY = 250;
fx = new Vector3D*[pointsX];
for(int x = 0; x < pointsX; ++x) {
fx[x] = new Vector3D[pointsY];
}
thetaX = 0;
thetaY = 0;
thetaZ = 0;
for(int y = 0; y < pointsY; y++) {
for(int x = 0; x < pointsX; x++) {
fx[x][y].x = x * (xMax*2)/pointsX - xMax;
fx[x][y].y = y * (yMax*2)/pointsY - yMax;
/* UN COMMENT ANY ONE OF THE BELOW FUNCTIONS OF X,Y */
// fx[x][y].z = 0;
// fx[x][y].z = pow(fx[x][y].x/20,2) + pow(fx[x][y].y/20, 2) - 100; // z = x^2 + y^2;
// fx[x][y].z = 30*sin(fx[x][y].x/20) + -15*cos(fx[x][y].y/20); // z = sin(x) - cos(x);
// fx[x][y].z = pow(fx[x][y].x/20,2) + pow(fx[x][y].y/20, 2); // z = x^2 + y^2;
// fx[x][y].z = sqrt(230*230 - pow(fx[x][y].x,2) - pow(fx[x][y].y, 2)); // x^2 + y^2 + z^2 = r^2
// fx[x][y].z = 20*log( sqrt(200*200 - pow(fx[x][y].x/2,2)) - 20*log( pow(fx[x][y].y/2,2)) );
// fx[x][y].z = 20*log(pow(fx[x][y].x/2,2))- 20*log( pow(fx[x][y].y/2,2));
// fx[x][y].z = (20*log(pow(fx[x][y].x/2,2)+ pow(fx[x][y].y/2,2))) -200;
// fx[x][y].z = (pow(fx[x][y].x/80, fx[x][y].x/20) - pow(fx[x][y].y/80, fx[x][y].y/20)) -200;
// fx[x][y].z = (pow(fx[x][y].x/25, fx[x][y].x/25) + pow(fx[x][y].y/25, fx[x][y].y/25)) /*- log(fx[x][y].x + fx[x][y].y)*/ -200;
// fx[x][y].z = 20*log(fx[x][y].x)/100 - 20*pow(fx[x][y].y/100, 2);
// fx[x][y].z = pow(fx[x][y].x/2,2)+ 1/pow(fx[x][y].y/2,2);
// fx[x][y].z = 10*tan(fx[x][y].x/40) + -10*tan(fx[x][y].y/40); // z = sin(x) - cos(x);
// fx[x][y].z = 30 / ( pow(fx[x][y].x/20,1) + pow(fx[x][y].y/20, 1)); // z = x^2 + y^2;
// fx[x][y].z = 30 / ( pow(fx[x][y].x/20,1) + pow(fx[x][y].y/20, 1)); // z = x^2 + y^2;
// fx[x][y].z = pow(fx[x][y].x/20,2) - pow(fx[x][y].y/20, 2) + (20*log(pow(fx[x][y].x/2,2)+ pow(fx[x][y].y/2,2))) - 100;
// fx[x][y].z = 30*sin(fx[x][y].x/40) + -15*cos(fx[x][y].y/40) + (20*log(pow(fx[x][y].x/2,2)+ pow(fx[x][y].y/2,2))) - 100;
// fx[x][y].z = -(pow(fx[x][y].x/20,2) + pow(fx[x][y].y/20, 2) )+ (40*log(pow(fx[x][y].x,2) - pow(fx[x][y].y,2))) - 175;
// fx[x][y].z = tan(fx[x][y].x)*tan(fx[x][y].y);
// fx[x][y].z = tan(fx[x][y].x)*fx[x][y].x*tan(fx[x][y].y);
// fx[x][y].z = tan(fx[x][y].x)*fx[x][y].x*tan(fx[x][y].y)*fx[x][y].y;
// fx[x][y].z = sin(fx[x][y].x/30)*fx[x][y].x*cos(fx[x][y].y/30)*fx[x][y].y/100;
fx[x][y].z = sin(fx[x][y].x/30)*fx[x][y].x*cos(fx[x][y].y/30)*fx[x][y].y/100 + 40*log(pow(fx[x][y].x/2,2) + pow(fx[x][y].y/2,2)) - 200;
// fx[x][y].z = abs((long)(sin(fx[x][y].x/30)*fx[x][y].x*cos(fx[x][y].y/30)*fx[x][y].y/100));
// fx[x][y].z = sin(log(fx[x][y].x/30))*fx[x][y].x*cos(log(fx[x][y].y/30))*fx[x][y].y/100;
// fx[x][y].z = 30 * acosf(fx[x][y].x/20) - 30 * asinf(fx[x][y].y/20);
}
}
for(int y = 0; y < pointsY; y++) {
for(int x = 0; x < pointsX; x++) {
fx[x][y] = rotateX(fx[x][y], PI/4);
fx[x][y] = rotateY(fx[x][y], -PI/5);
fx[x][y] = rotateZ(fx[x][y], 0);
}
}
xaxis = 320;
yaxis = 240;
bool done = false;
while (!done) {
SDL_Event event;
while (SDL_PollEvent(&event)) {
switch (event.type) {
case SDL_QUIT:
done = true;
break;
case SDL_KEYDOWN:
KEYS[event.key.keysym.sym] = true;
break;
case SDL_KEYUP:
KEYS[event.key.keysym.sym] = false;
thetaX = 0;
thetaY = 0;
thetaZ = 0;
break;
}
}
bool rot = false;
if(KEYS[SDLK_q]) {
thetaX = -rotSpeed;
rot = true;
}
if(KEYS[SDLK_w]) {
thetaX = rotSpeed;
rot = true;
}
if(KEYS[SDLK_a]) {
thetaY = -rotSpeed;
rot = true;
}
if(KEYS[SDLK_s]) {
thetaY = rotSpeed;
rot = true;
}
if(KEYS[SDLK_z]) {
thetaZ = -rotSpeed;
rot = true;
}
if(KEYS[SDLK_x]) {
thetaZ = rotSpeed;
rot = true;
}
if(KEYS[SDLK_LEFT]) {
xaxis -= 10;
}
if(KEYS[SDLK_RIGHT]) {
xaxis += 10;
}
if(KEYS[SDLK_UP]) {
yaxis -= 3;
}
if(KEYS[SDLK_DOWN]) {
yaxis += 3;
}
if(KEYS[SDLK_ESCAPE]) {
done = true;
}
if(rot) {
rot = false;
for(int y = 0; y < pointsY; y++) {
for(int x = 0; x < pointsX; x++) {
fx[x][y] = rotateX(fx[x][y], thetaX);
fx[x][y] = rotateY(fx[x][y], thetaY);
fx[x][y] = rotateZ(fx[x][y], thetaZ);
}
}
}
SDL_FillRect(screen, 0, SDL_MapRGB(screen->format, 0, 0, 0));
for(int y = 0; y < pointsY; y++) {
for(int x = 0; x < pointsX; x++) {
setPixel(screen, fx[x][y].x + xaxis, fx[x][y].y + yaxis, SDL_MapRGB(screen->format, 255,255,255));
}
}
SDL_Flip(screen);
}
printf("Exited cleanly\n");
return 0;
}
/**
* 0 to 255
*/
static double sigmoid(double x) {
return 255.0 / (1 + exp(-x));
}
void setPixel(SDL_Surface* surface, int x, int y, Uint32 pixel) {
if(surface == NULL) {
cout << "Failed to set pixel, surface not initialized!"<< endl;
return;
}
if(x < 0 || x >= surface->w || y < 0 || y >= surface->h) {
// cout << "Pixel not within surface's dimensions"<< endl;
return;
}
int bpp = surface->format->BytesPerPixel;
/* p is the address to the pixel we want to set */
Uint8 *p = (Uint8 *)surface->pixels + y * surface->pitch + x * bpp;
switch(bpp) {
case 1:
*p = pixel;
break;
case 2:
*(Uint16 *)p = pixel;
break;
case 3:
if(SDL_BYTEORDER == SDL_BIG_ENDIAN) {
p[0] = (pixel >> 16) & 0xff;
p[1] = (pixel >> 8) & 0xff;
p[2] = pixel & 0xff;
} else {
p[0] = pixel & 0xff;
p[1] = (pixel >> 8) & 0xff;
p[2] = (pixel >> 16) & 0xff;
}
break;
case 4:
*(Uint32 *)p = pixel;
break;
}
}
Vector3D.h
#ifndef __VECTOR_3D_H__
#define __VECTOR_3D_H__
#include "math.h"
/*
3D Vector and rotation functions. Rotations about X, Y, Z, and any arbitrary Vector
*/
#define PI 3.14159265358979323846264338327950288
struct Vector3D {
double x;
double y;
double z;
};
static Vector3D& rotateX(struct Vector3D &Vector, double theta);
static Vector3D& rotateY(struct Vector3D &vector, double theta);
static Vector3D& rotateZ(struct Vector3D &vector, double theta);
static Vector3D& getUnitVector3D(struct Vector3D &vector);
static Vector3D& rotateAroundVector3D(struct Vector3D &vect1, struct Vector3D &vect2, double theta);
static double degToRad(double deg);
/**
* [(1 ,0 ,0),
* (0 ,cos(a) ,-sin(a)),
* (0 ,sin(a) ,cos(a))]
* @param Vector3D
* @param theta
*/
Vector3D& rotateX(struct Vector3D &vector, double theta) {
Vector3D newv;
newv.x = vector.x;
newv.y = vector.y * cos(theta) + vector.z * -sin(theta);
newv.z = vector.y * sin(theta) + vector.z * cos(theta);
return newv;
}
/**
* [(cos(a) ,0 ,sin(a)),
* (0 ,1 ,0),
* (-sin(a),0 ,cos(a))]
* @param Vector3D
* @param theta
*/
Vector3D& rotateY(struct Vector3D &vector, double theta) {
Vector3D newv;
newv.x = vector.x * cos(theta) + vector.z * sin(theta);
newv.y = vector.y;
newv.z = vector.x * -sin(theta) + vector.z * cos(theta);
return newv;
}
/**
* [(cos(a),-sin(a),0),
* (sin(a),cos(a) ,0),
* (0 ,0 ,1)]
* @param Vector3D
* @param theta
*/
Vector3D& rotateZ(struct Vector3D &vector, double theta) {
Vector3D newv;
newv.x = vector.x * cos(theta) + vector.y * -sin(theta);
newv.y = vector.x * sin(theta) + vector.y * cos(theta);
newv.z = vector.z;
return newv;
}
/**
* returns a unit vector
*/
Vector3D& getUnitVector3D(struct Vector3D &vector) {
Vector3D newv;
double d = sqrt(vector.x * vector.x + vector.y * vector.y + vector.z * vector.z);
newv.x = vector.x / d;
newv.y = vector.y / d;
newv.z = vector.z / d;
return newv;
}
/**
* using quaternions to rotate around an arbirtuary axis
* Given angle theta in radians and unit vector u = ai + bj + ck or (a,b,c)
*
* q0 = cos(r/2), q1 = sin(r/2) a, q2 = sin(r/2) b, q3 = sin(r/2) c
*
* Q =
* [
* (q0^2 + q1^2 - q2^2 - q3^2) 2(q1q2 - q0q3) 2(q1q3 + q0q2)
* 2(q2q1 + q0q3) (q0^2 - q1^2 + q2^2 - q3^2) 2(q2q3 - q0q1)
* 2(q3q1 - q0q2) 2(q3q2 + q0q1) (q0^2 - q1^2 - q2^2 + q3^2)
* ]
*
* Q u = u
*
* @param Vector3D 1
* @param Vector3D 2
* @param theta
* @return Vector
*/
Vector3D& rotateAroundVector(Vector3D &vect1, Vector3D &vect2, double theta) {
Vector3D newv;
Vector3D unit = getUnitVector3D(vect2);
//theta = Math.toRadians(theta);
double q0 = cos(theta/2);
double q1 = sin(theta/2)*unit.x;
double q2 = sin(theta/2)*unit.y;
double q3 = sin(theta/2)*unit.z;
// column vect
newv.x = (q0*q0 + q1*q1 - q2*q2 - q3*q3)* + 2*(q2*q1 + q0*q3) * vect1.y + 2*(q3*q1 - q0*q2) * vect1.z;
newv.y = 2*(q1*q2 - q0*q3)*vect1.x + (q0*q0 - q1*q1 + q2*q2 - q3*q3) * vect1.y + 2*(q3*q2 + q0*q1) * vect1.z;
newv.z = 2*(q1*q3 + q0*q2)*vect1.x + 2*(q2*q3 - q0*q1) * vect1.y + (q0*q0 - q1*q1 - q2*q2 + q3*q3) * vect1.z;
return newv;
}
double degToRad(double deg) {
return deg * PI / 180;
}
#endif
 Arrived
Arrived
 Ninja Turdle
Ninja Turdle