Ray Casting - Polygon Containment
Even before I learned the word algorithm, I have always enjoyed exacting solutions to problems. Particularly, I love very visual algorithms. Such algorithms include the symmetry, and also indirectness that you see when solving a Rubik's Cube and other spatial puzzles. These puzzles certainly have formal grammars and systems defining these patterns, yet I was initially attracted to the visual "truth" of the solutions I found.
I unexpectedly found another such "puzzle" when I was building a reverse geocoding service. My first round with the service was to perform city lookup. In this scenario, since cities can be represented as points, a GeoHash lookup was the optimal solution.
However, what about checking to see if a geo coordinate is contained within a polygon? This polygon could be a country, a province, a county, or any custom area. We can make a GeoHash work with a few modifications. But there is another way to check for polygon containment.
Ray Casting
Upon discovering this simple but effective algorithm many years back, I was excited to finally put it to some use. Note that this algorithm is also sometimes referred to as the Even-Odd Rule. I prefer to call it Ray Casting as we will literally be casting a ray (vector), and then applying the even-odd rule to determine containment of some point within the polygon. I have also found that this algorithm is intuitive enough to excite people who aren't familiar with algorithms.
The steps of the algorithm are simple.
- Pick a point that is obviously outside the solution space. For example, in the case of latitude and longitude points, we would select a point that is outside of the valid coordinate range. e.g.
(-987.654, -876.543). This is the point where we will cast our ray from. - Next we will draw a line from the cast point defined in step 1. to the point we want to test.
- We will count how many lines in the polygon our ray intersects with. If the count is odd, the point is inside the polygon; if even, the point is outside.
Example with Square
First we will begin with a trivial example, a square. The square is denoted by blue lines and dots. We have a point p that we want to determine whether or not it is inside the square. We will cast our ray from a place to the left of the square. It is important that this ray be placed in a spot that is guaranteed to not exist in the polygon.
fig 1.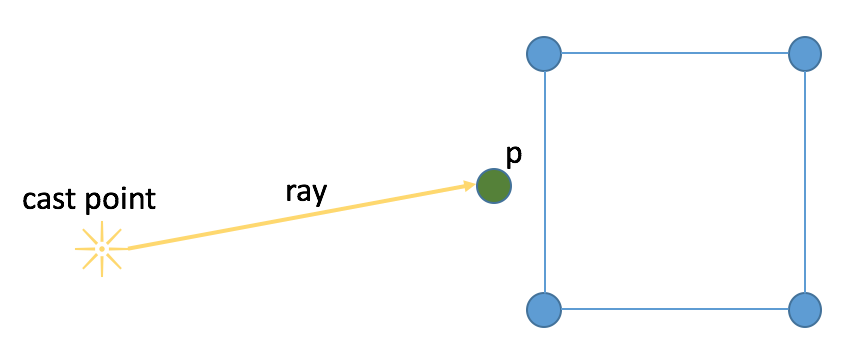
In fig 1, the ray travels from the cast point to point p without intersecting a single line of the square. The intersection count is zero, which is even, therefore the point is outside the square.
fig 2.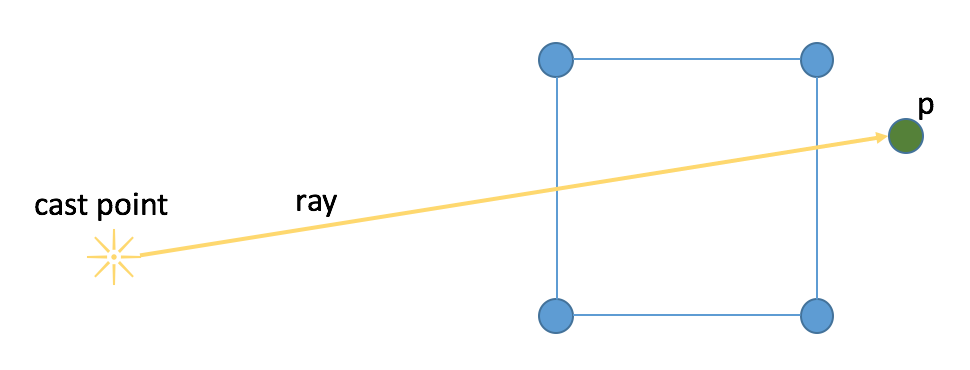
We will next look at an example where the point p lies to the right of the square. Our ray intersects two lines in the square, which is even, therefore the point is outside the square.
fig 3.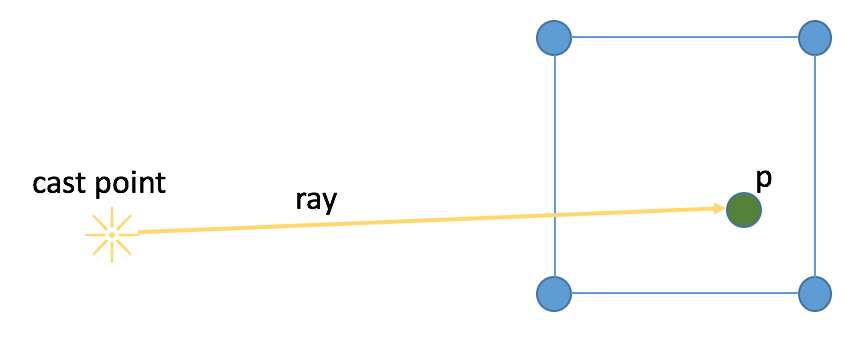
Our next example will be a point that lies in the square as illustrated in fig 3. Tracing our ray shows that it intersected with exactly one side of the square, which is odd, therefore our point is inside the square.
Example with Polygon
fig 4.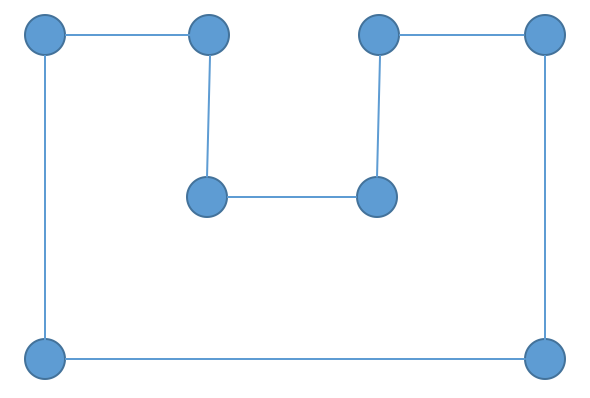
Next we will apply the algorithm to a more complex polygon illustrated above in fig 4.
fig 5.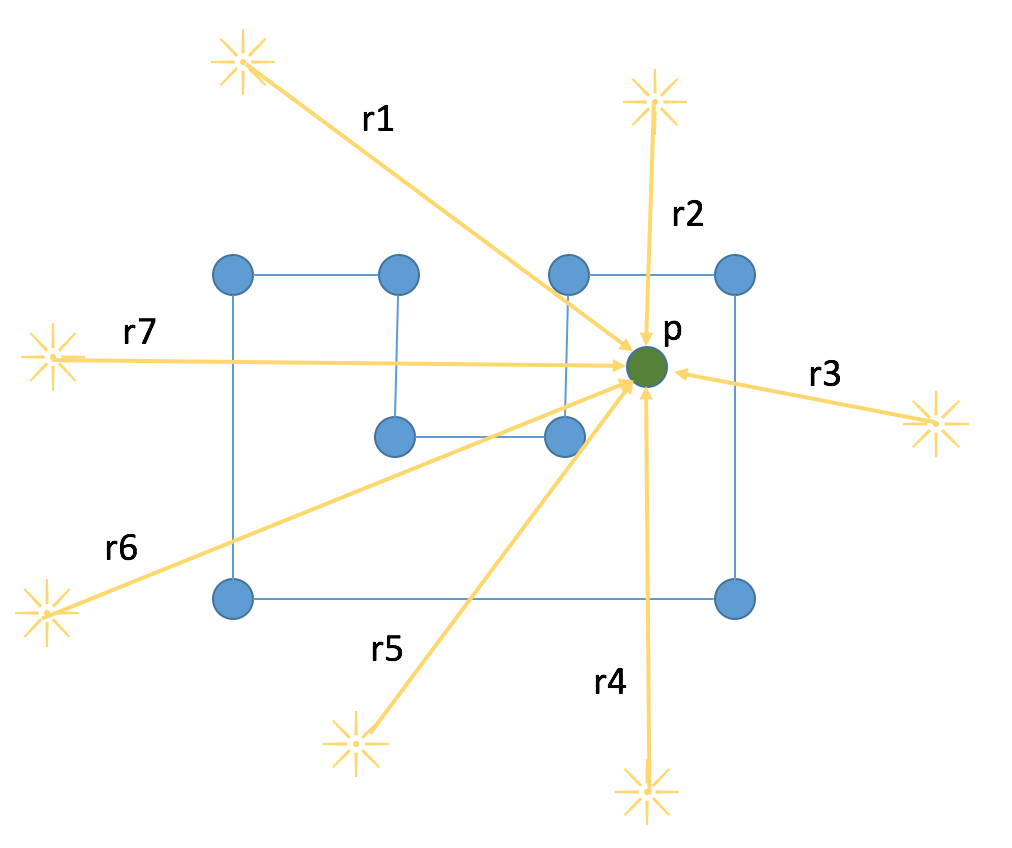
For this test we are going to start with a point p that is soundly located inside the polygon, and cast a series of rays from outside to point p and count the number of times each ray intersects with a line in the polygon. If our algorithm holds, each ray will intersect with an odd number of lines. Each of the rays are labeled in fig 5.
| Ray | Intersections |
| r1 | 1 |
| r2 | 1 |
| r3 | 1 |
| r4 | 1 |
| r5 | 1 |
| r6 | 3 |
| r7 | 3 |
It seems our luck holds. As expected, each ray intersects with our polygon an odd number of times. Each verifying that the point is inside the polygon.
fig 6.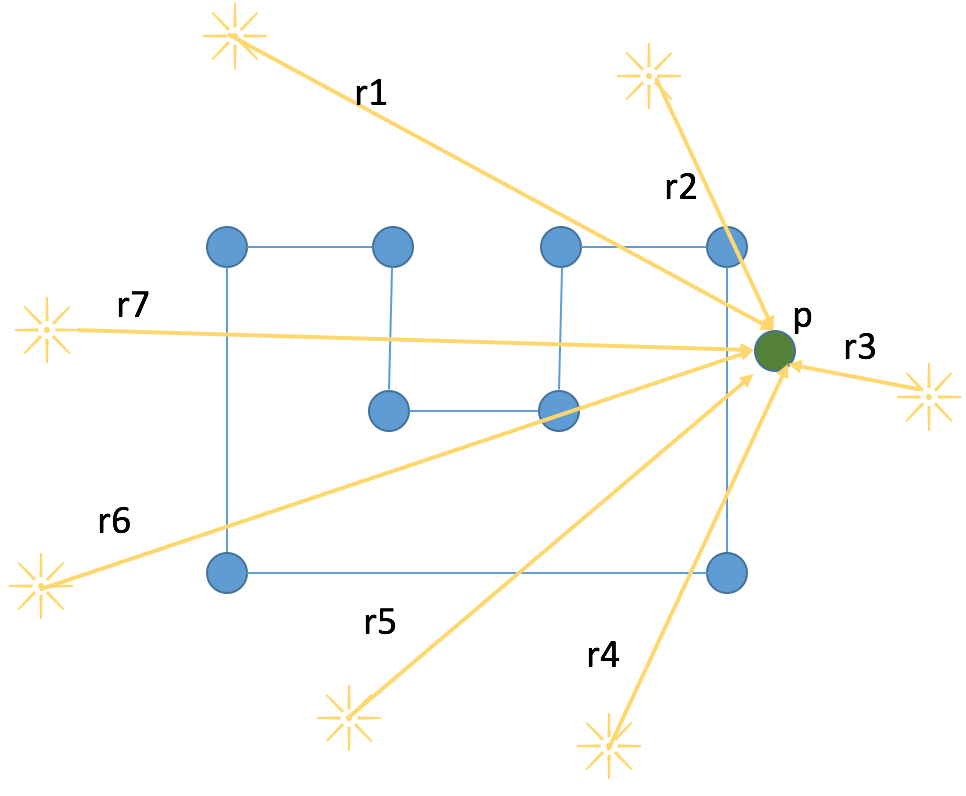
Next, we will place point p outside of the polygon as seen in fig 6. Once again, we will cast rays from external points to point p and test our hypothesis that the number of intersections with the polygon should be even.
| Ray | Intersections |
| r1 | 2 |
| r2 | 0 |
| r3 | 0 |
| r4 | 2 |
| r5 | 2 |
| r6 | 2 |
| r7 | 4 |
Assuming our counting is correct, the algorithm holds true. Each ray intersects with our polygon an even number of times. Each verifying that the point is outside the polygon.
Other Polygon types.
So far we have demonstrated Ray Casting with a simple concave and convex polygon. Ray Casting also works with complex polygons such as self-intersecting polygons and even polygons with holes in them.
Pitfalls
As with any algorithm, you can't have your cake and eat it too.
Performance
The algorithm itself is a bit slow. It runs in O(n) as you have to check every line in the polygon. If you have m polygons, then it becomes m * O(n). Given complex polygons such as high resolution polygons used to describe country or province boundaries, n can approach or even surpass m, and it approaches O(n^2).
A solution to this is to not use high resolution geo polygons. Chances are you can achieve high accuracy even with low resolution polygons. Another options is to use GeoHashing techniques mentioned above, but they too incur their own costs, usually in terms of space/memory.
Another critical optimization is to calculate a bounding rectangle when you are processing the polygon data. You can do this by storing the (min_x, min_y) and the (max_x, max_y). Once you have obtained a bounding rectangle, you should first perform rectangle containment before performing the expensive polygon containment check. Rectangle containment is substantially cheaper in practice. This will be demonstrated below.
Vertex Intersection
A ray may intersect a vertex in the polygon. Does this mean the ray intersected with a line or not? There is no correct answer to this and it is up to the application to determine how to handle this. That said, there are ways to decrease the chance of a ray intersecting with a vertex. The method I employ is to set the ray cast point to something obscure and with multiple decimal places. e.g. (-987.654, -876.543).
An example can be constructed of a square located at (1, 1), (2, 1), (2, 2), (1, 2) and point p is located in the center of the square at (1.5, 1.5). If a ray is cast from the origin, (0, 0), then it will overlap with the vertex located at (1, 1). By simply offsetting the ray cast point to something obscure like above, it won't overlap.
It should also be noted that dealing with real data like geo coordinates, such an artificial construct is less likely to happen and you will still have to figure out how you want to count vertex intersection. In many cases it's easy enough to just ignore and accept the error.
Java Code
/**
* Apply the even-odd rule for a ray-cast from an external reference (bottom corner)
* based on how many lines it intersects with a given polygon.
*
* Polygons should not be self-intersecting polygons.
* odd = in polygon
* even = outside polygon
*/
public class RayCasting {
// this point is to determine where to start casting from.
// e.g. in a 2d grid where all values are positive, the origin (0,0) is a safe start.
// e.g. with lat/lon you should start outside the valid range for lat/lon to
// guarantee you do not start casting a ray from within the polygon!
private final Point rayStartPoint;
public RayCasting(final Point rayStartPoint) {
this.rayStartPoint = rayStartPoint;
}
public boolean contains(final Point point, final Polygon polygon) {
if (polygon.points.size() < 3) {
throw new IllegalStateException("Polygons must have at least 3 points.");
}
// first do a handy-dandy rectangle contains check so we don't waste time
// computing intersections on each line in the polygon
if (!contains(polygon.bounds, point)) { return false; }
int intersections = 0;
// walk all vertices of polygon
for (int i = 0; i < polygon.points.size() - 1; i++) {
if (isIntersects(point, polygon.points.get(i), polygon.points.get(i + 1))) {
intersections++;
}
}
// don't forget the tail-front end connection!
if (isIntersects(point,
polygon.points.get(polygon.points.size() - 1),
polygon.points.get(0))) {
intersections++;
}
return intersections % 2 != 0; // odd-in / even-out
}
// use already existing java libraries for line intersection
private boolean isIntersects(final Point testPoint,
final Point p1,
final Point p2) {
return Line2D.linesIntersect(
rayStartPoint.getX(), rayStartPoint.getY(),
testPoint.getX(), testPoint.getY(),
p1.getX(), p1.getY(), p2.getX(), p2.getY());
}
// our cheap rectangle collision method.
private boolean contains(final Rectangle rectangle, final Point point) {
return point.getX() >= rectangle.getX() &&
point.getY() >= rectangle.getY() &&
point.getX() <= rectangle.getX() + rectangle.getWidth() &&
point.getY() <= rectangle.getY() + rectangle.getHeight();
}
}
The core data structures used in the algorithm.
/**
* A polygon that is aware of it's min/max x/y coords
*/
public class Polygon {
public final List<Point> points;
// outer rectangular bounds of polygon
public final Rectangle bounds;
public Polygon(final Point... points) {
this.points = Arrays.asList(points);
this.bounds = calculateMinMaxBounds(this.points);
}
public Polygon(final List<Point> points) {
this.points = points;
this.bounds = calculateMinMaxBounds(this.points);
}
// used for our optimization mentioned above.
private static Rectangle calculateMinMaxBounds(final List<Point> points) {
double minX = Double.MAX_VALUE;
double minY = Double.MAX_VALUE;
double maxX = Double.MIN_VALUE;
double maxY = Double.MIN_VALUE;
for (final Point point : points) {
if (point.getX() < minX) { minX = point.getX(); }
if (point.getY() < minY) { minY = point.getY(); }
if (point.getX() > maxX) { maxX = point.getX(); }
if (point.getY() > maxY) { maxY = point.getY(); }
}
return new Rectangle(minX, minY, maxX - minX, maxY - minY);
}
}
Our custom Point class (using doubles)
public class Point {
private final double x;
private final double y;
public Point(final double x, final double y) {
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public double getY() {
return y;
}
}
A nice unit test to wrap everything up.
public class RayCastingTest {
// start ray casting from a fairly random start point to avoid vertex overlap
// for trivial test cases. vertex overlap is much less likely in real geo cases,
// and should occur infrequently enough to ignore.
private static final RayCasting RAY_CASTING = new RayCasting(
new Point(-1.123456789, -1.987654321));
@Test
public void square() {
final Polygon square = new Polygon(
new Point(1.0, 1.0),
new Point(2.0, 1.0),
new Point(2.0, 2.0),
new Point(1.0, 2.0));
// center of square
assertTrue(RAY_CASTING.contains(new Point(1.5, 1.5), square));
// other side of square
assertFalse(RAY_CASTING.contains(new Point(2.5, 1.5), square));
}
@Test
public void weirdShape() {
// the ultimate shape, 凹
final Polygon 凹 = new Polygon(
new Point(1.0, 1.0),
new Point(4.0, 1.0),
new Point(4.0, 3.0),
new Point(3.0, 3.0),
new Point(3.0, 2.0),
new Point(2.0, 2.0),
new Point(2.0, 3.0),
new Point(1.0, 3.0));
// inside 凹
assertTrue(RAY_CASTING.contains(new Point(1.5, 1.5), 凹));
assertTrue(RAY_CASTING.contains(new Point(1.5, 2.5), 凹));
assertTrue(RAY_CASTING.contains(new Point(2.0, 1.5), 凹));
assertTrue(RAY_CASTING.contains(new Point(2.5, 1.5), 凹));
assertTrue(RAY_CASTING.contains(new Point(3.5, 1.5), 凹));
assertTrue(RAY_CASTING.contains(new Point(3.5, 2.5), 凹));
// outside of 凹
assertFalse(RAY_CASTING.contains(new Point(1.5, 3.5), 凹));
assertFalse(RAY_CASTING.contains(new Point(2.5, 2.5), 凹));
assertFalse(RAY_CASTING.contains(new Point(3.5, 3.5), 凹));
assertFalse(RAY_CASTING.contains(new Point(4.5, 0.5), 凹));
assertFalse(RAY_CASTING.contains(new Point(4.5, 1.0), 凹));
assertFalse(RAY_CASTING.contains(new Point(4.5, 1.5), 凹));
assertFalse(RAY_CASTING.contains(new Point(4.5, 2.0), 凹));
assertFalse(RAY_CASTING.contains(new Point(4.5, 2.5), 凹));
}
}
 Arrived
Arrived
 Ninja Turdle
Ninja Turdle