Cellular Automata - Pokemon Type Battle Simulation

The code can all be found on GitHub: here

This Cellular Automata (CA) builds up to a Pokemon Type battle simulation from simpler CA.

Simulations include:

• 1. A balanced 3 Typed CA (Fire, Water, Grass).
• 2. A larger, balanced N Typed CA.
• 3. The full Pokemon Type CA based on the strength/weakness/immunity charts of Gen 1 Pokemon games

#1 Balanced 3 Type Simulation (Fire, Water, Grass)

This demonstration is a CA that simulates three balanced Pokemon types battling against each other.

Balanced meaning that Type A can beat B, and only B. Type B can beat C, and only C. So on and so forth.

Rules for 3 Type Simulation

• Fire beats Grass.
• Grass beats Water.
• Water beats Fire.
• If neighboring cells are empty, the cell is occupied by the attacker.
• Each cell has a determined amount of HP to determine when it dies.
• Each loss, a cell loses one HP.
• Depending on mode, both the attacker and defender can mutually attack each other, else only the attacker attacks.

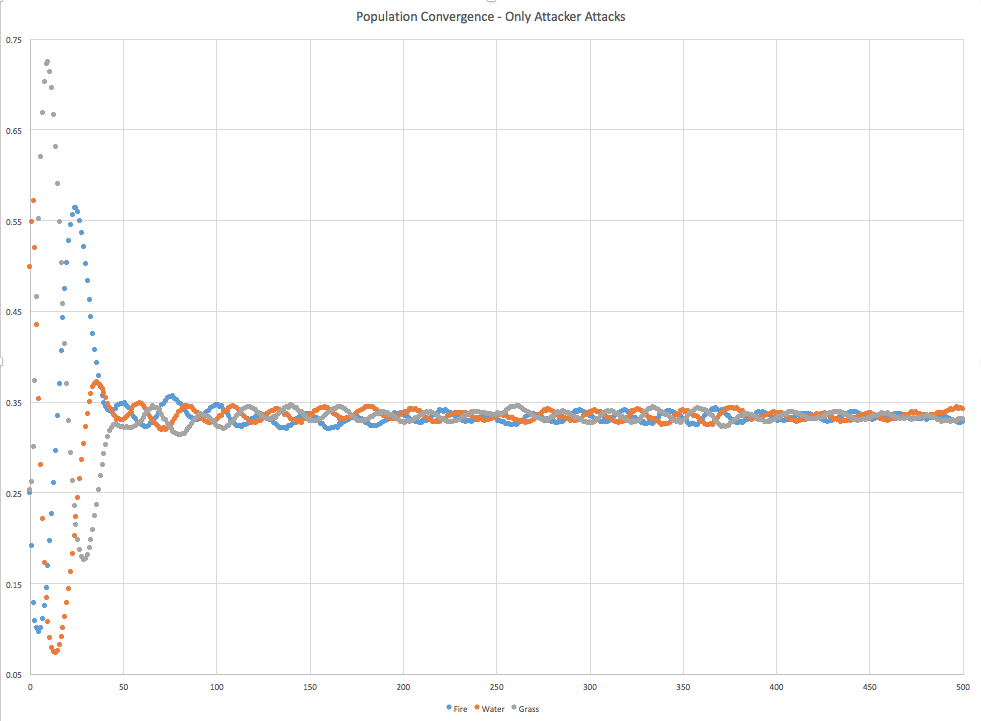
The below convergence graph shows how the populations starting from a random state tend towards homogeneousness. The end state is that each of the three elements represent approximately 33% of the occupied space. Note: The large variance in the beginning is because the map was initialized "sparsely" with a lot of empty space. All other experiments are "dense" with no empty space.

A video of a larger simulation: here

#2 Balanced N Type Simulation

This demonstration is very similar to demonstration #1 except for more than 3 types of balanced Pokemon types will compete with each other. The types are labeled "A" to "Z". The rules follow that "B" beats "A", "C" beats "B", ..., "Z" beats "A". In this simulation each cell is densely packed with no empty cell.

N Types Convergence

For low N, the types quickly converge to order and balance. With the exception being that 2 types, since they attack each other, tend to end with a single winner.

Another interesting trend is the "bulge" pattern that appears in the center of the convergence graphs. The population distribution starts out balanced and ends balanced. However, during these bulges, they are very off balance. The starting states are randomly initialized and could be described as "chaotic", and the end states are well "ordered" and portray obvious patterns. This could be thought of as the "energy" required to bring order to the chaos of the system.

It is possible for a type to "accidentally" go extinct, which brings the system out of balance. This imbalance can be seen more frequently when N = 2, or as N grows in size (~20+).

The 26 Typed CA tend to never escape the random initialization.

Below are the convergence charts for select N Typed simulations.

2 Type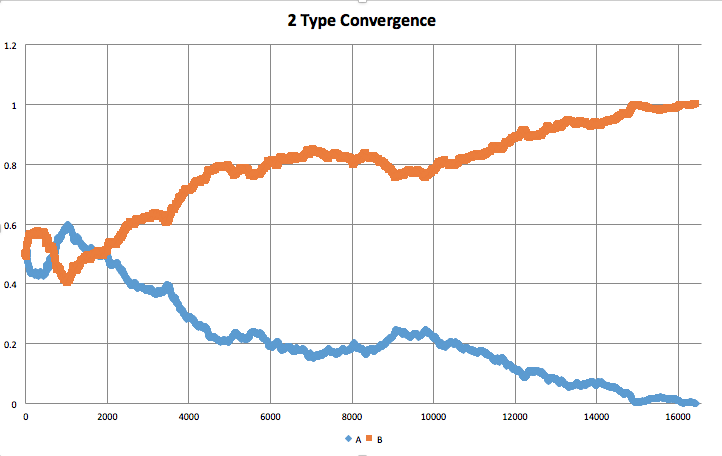	4 Type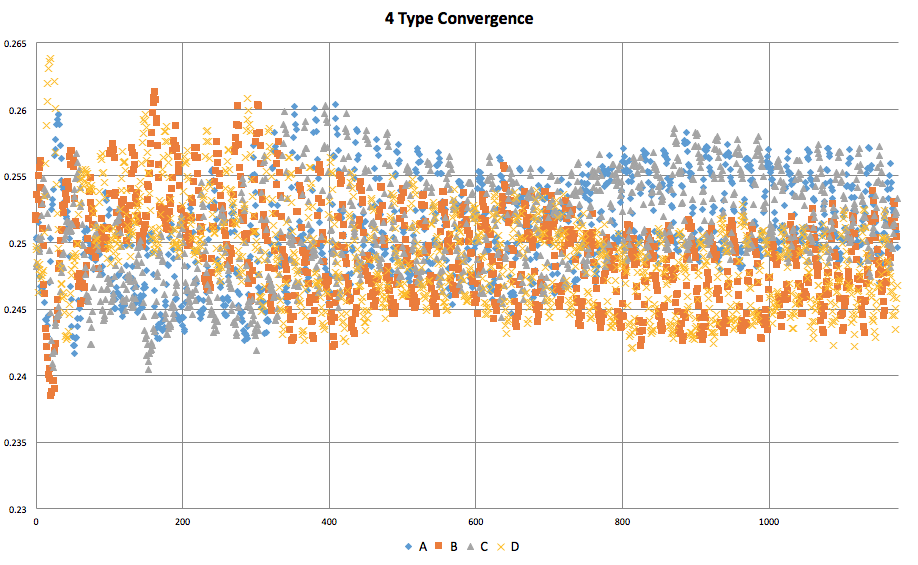
5 Type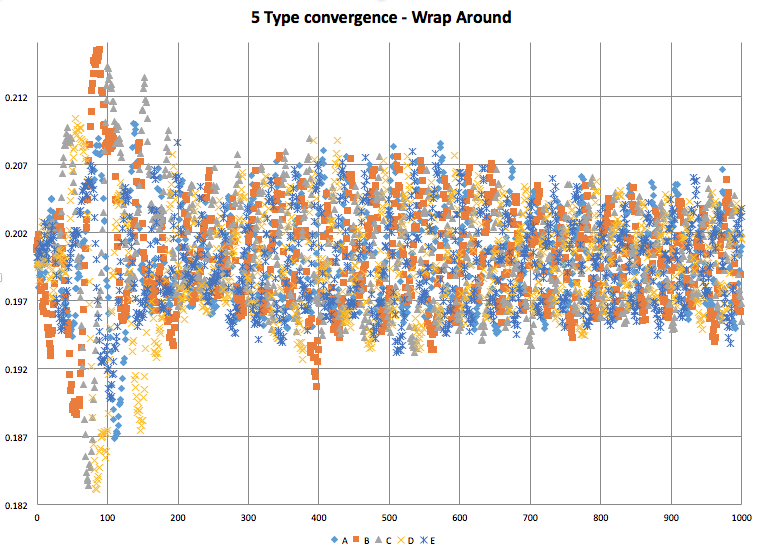	8 Type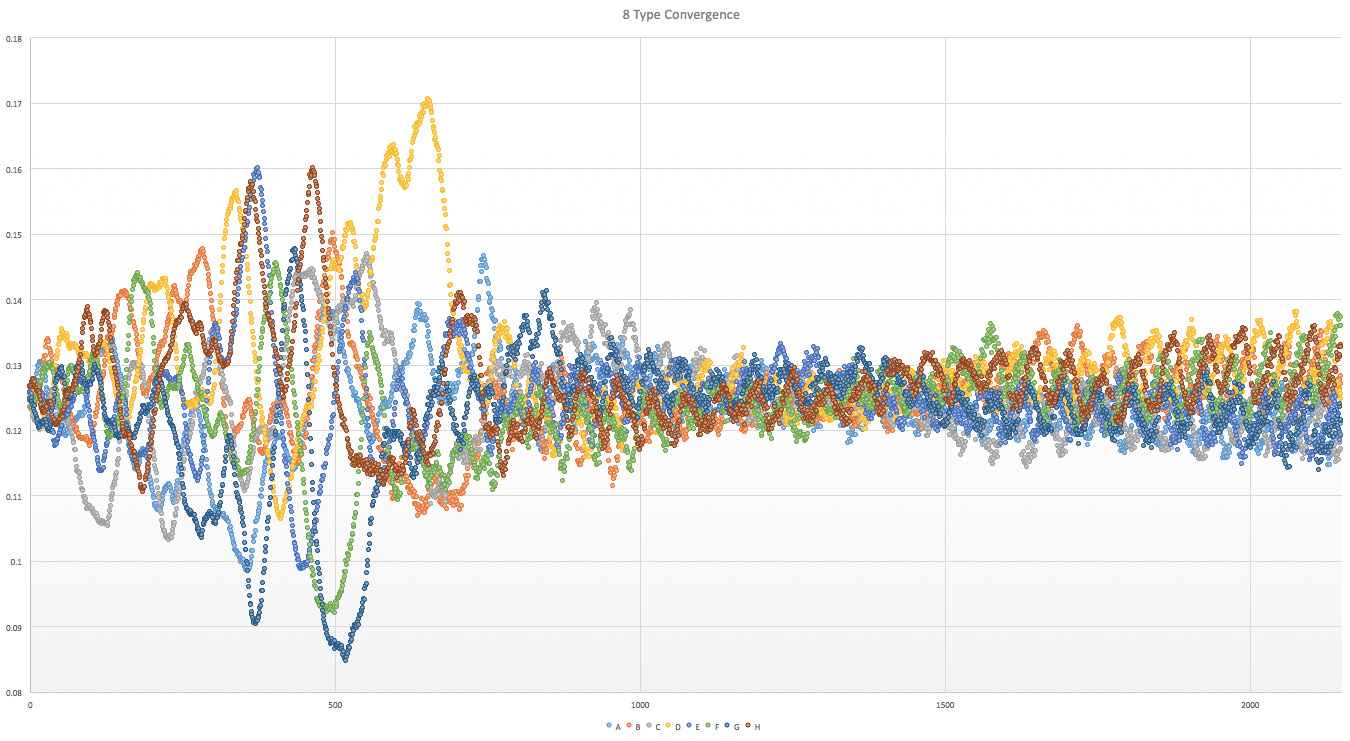
10 Type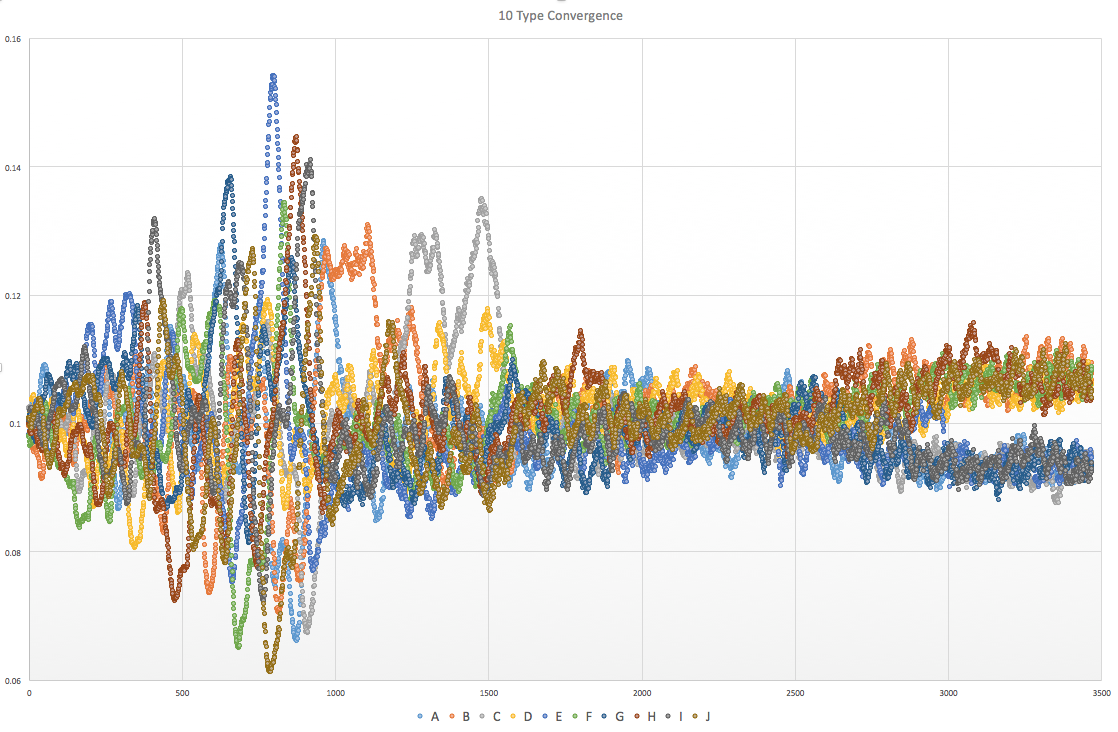	12 Type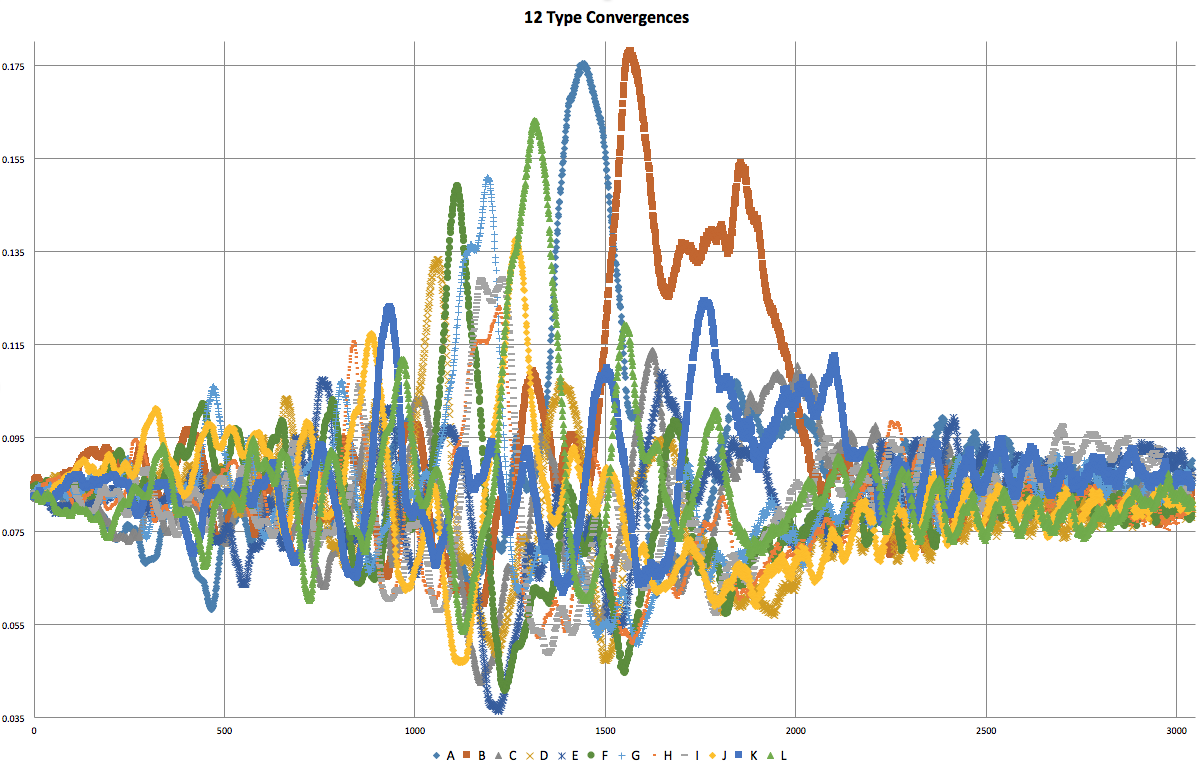
16 Type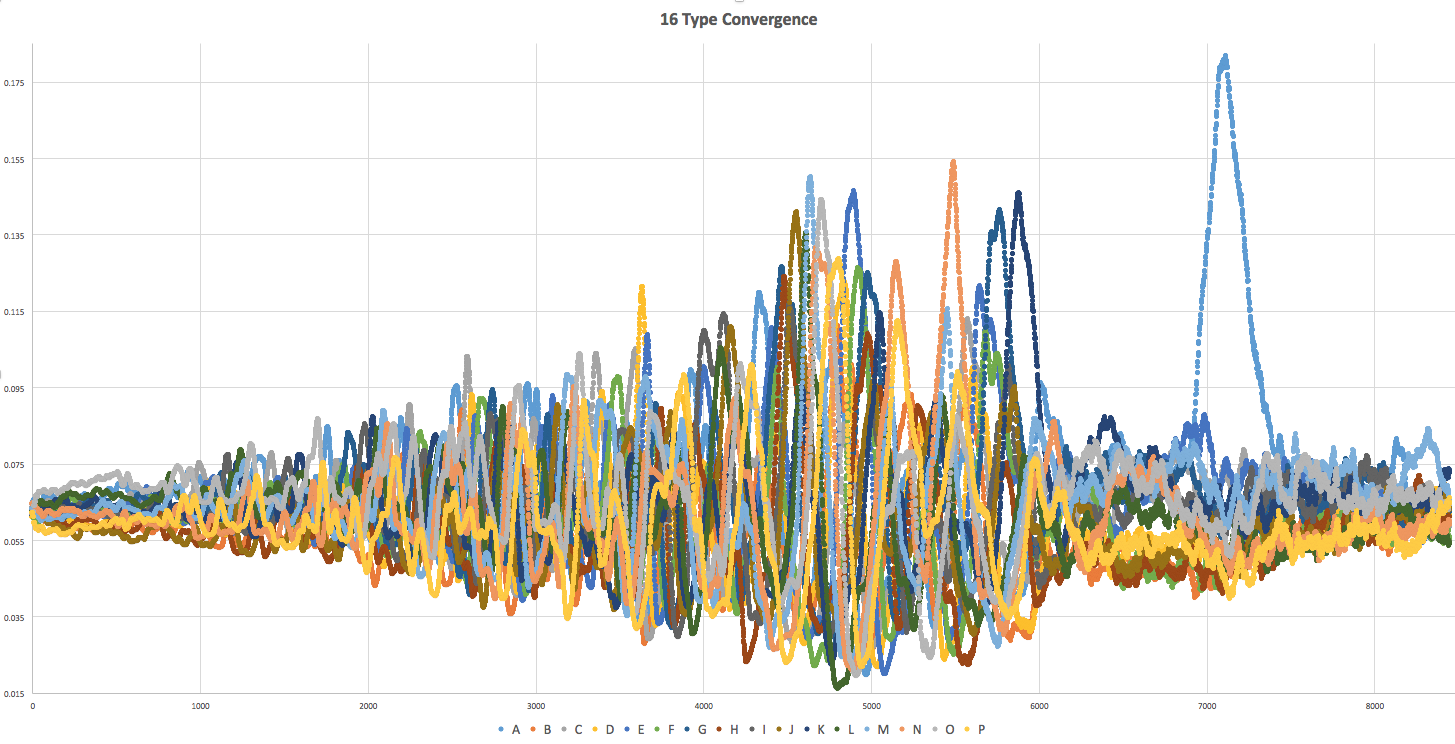	20 Type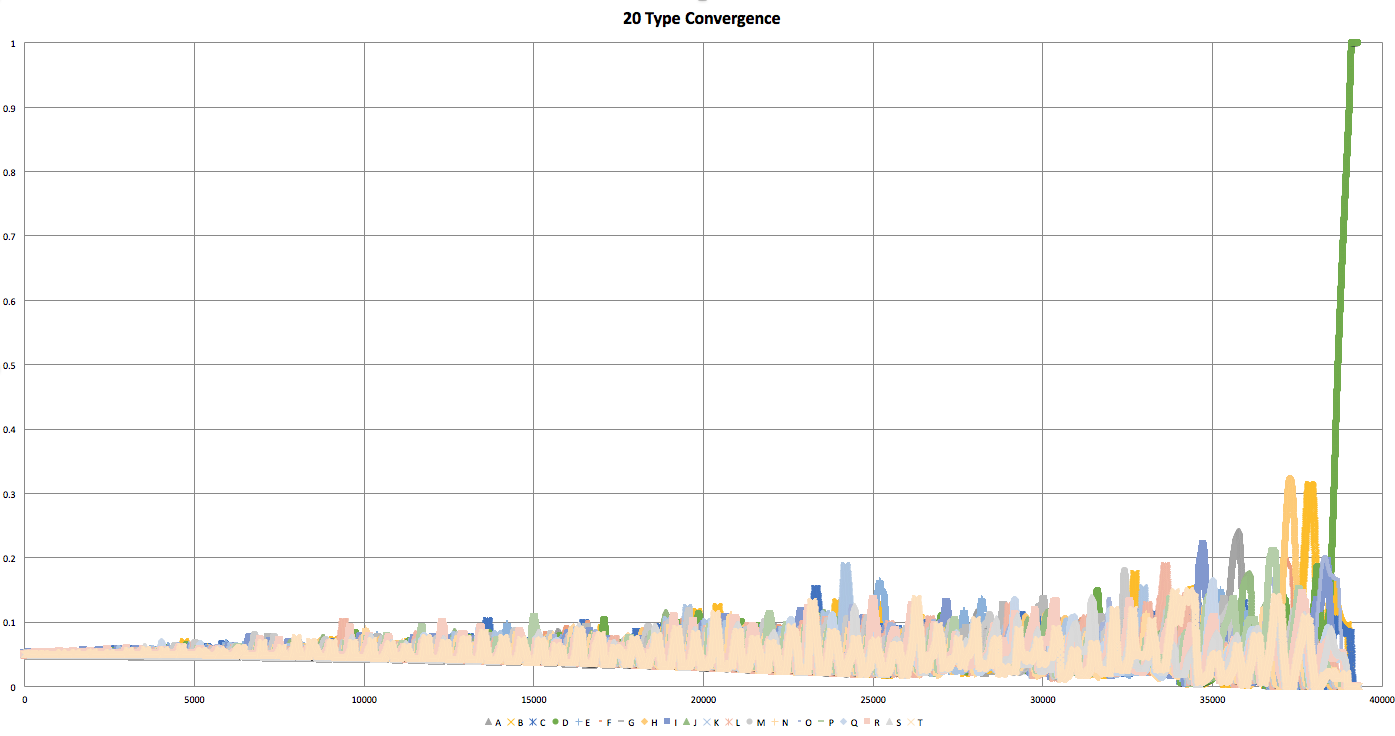

N Types GIFs

GIFs are large so I tried to not load all of them on one page. Below are some links (they open in new tabs).

4 Type CA, 8 Type CA, 10 Type CA, 12 Type CA, 20 Type CA

12 Typed CA

N Types Notable Images

• For large N (~20+) the likelihood of stagnation occurs, with little or no pattern emerging. It is also more likely that one type wins, and other types go extinct.

Note the clumps of randomly placed colors. Those represent Types that have remained stagnant since the the initialization of the simulation.

As mentioned above, large N Typed simulations have a hard time getting started due to the lower probability of having neighbors that they can win over. The below images show the formation of a hole that opened, and spread. Sadly however, the CA died a slow death as entropy won.

#3 Full CA Simulation using the Pokemon Gen 1 Types

This CA is a direct Type vs type simulation. It ignores all other variables, Such as:

• Each Pokemon's stats (attack, defense, hp) are exactly the same. In the game, a Dragon Pokemon has much higher stats than another type such as a Normal Pokemon.
• The distribution of each Pokemon is equal. Certain In the game, Pokemon types are more rare/common.
• A Pokemon will attack any neighboring Pokemon, regardless of the type, to include same typed Pokemon.

The full type system can be found here on Bulbapedia.

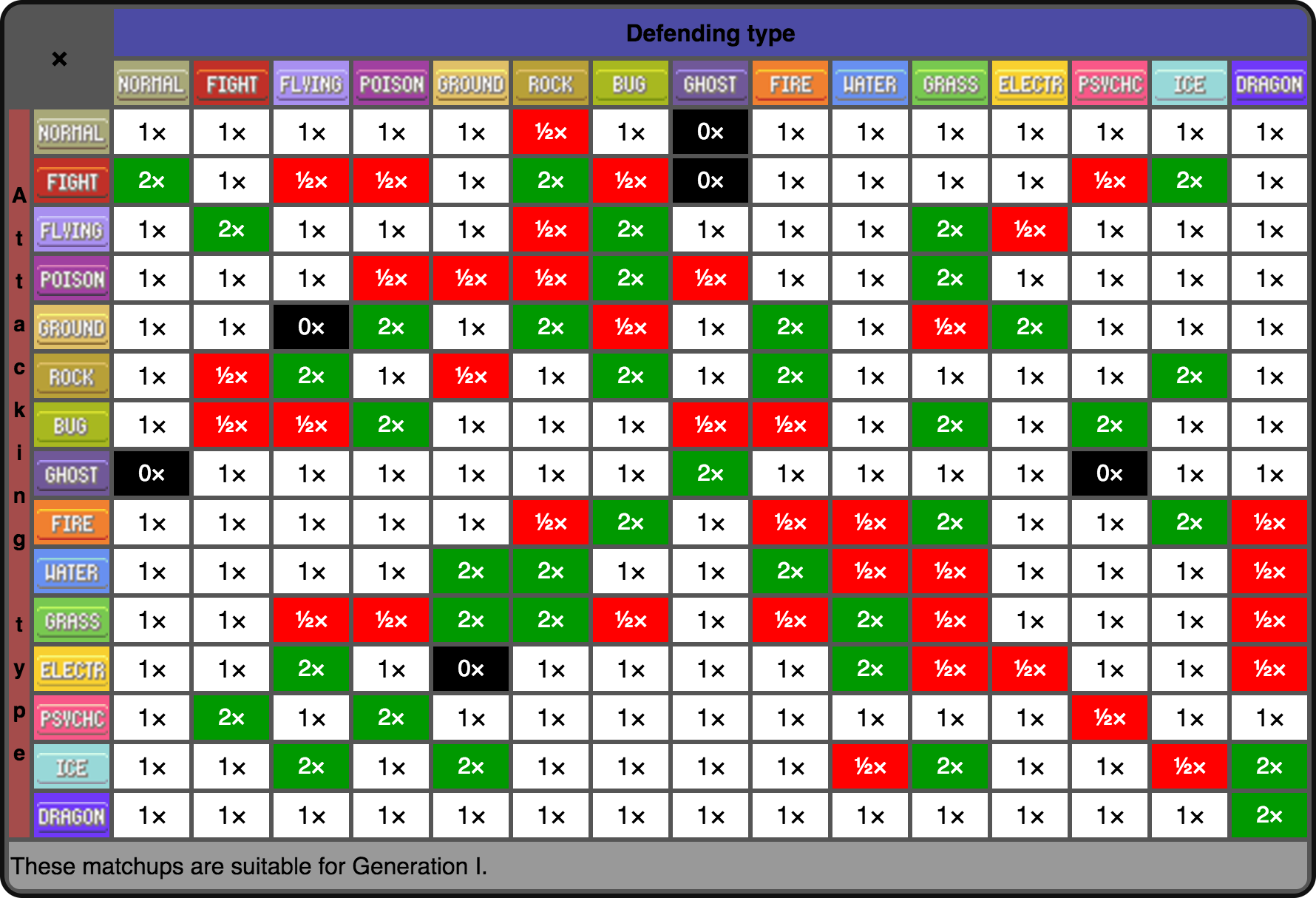
In this CA, an attacking Pokemon will attack each of it's neighbors. The damage delivered will be determined based on both the type of the attacker and the defender, per the above chart. For example Fire does 2x damage to Grass, and Normal does 0 damage to Ghost type because Ghost types are immune to physical attack.

Each color represents a type. The color mapping can be found in the source code.

2 minute intense simulation: here (Normal Wins)

A long simulation in which I eventually gave up hoping for a winner. However, 40 minutes later, Normal makes an epic comeback and starts conquering from the top right corner. (I did not have world-wrap at the time of this simulation)

Part 1, Part 2, Part 3, Part 4

The epic comeback of Normal

More GIFs in the below are some links (they open in new tabs).

Run 1

Run 2a, Run 2b

Run with no immunities

Sample Convergence Rates

Run 1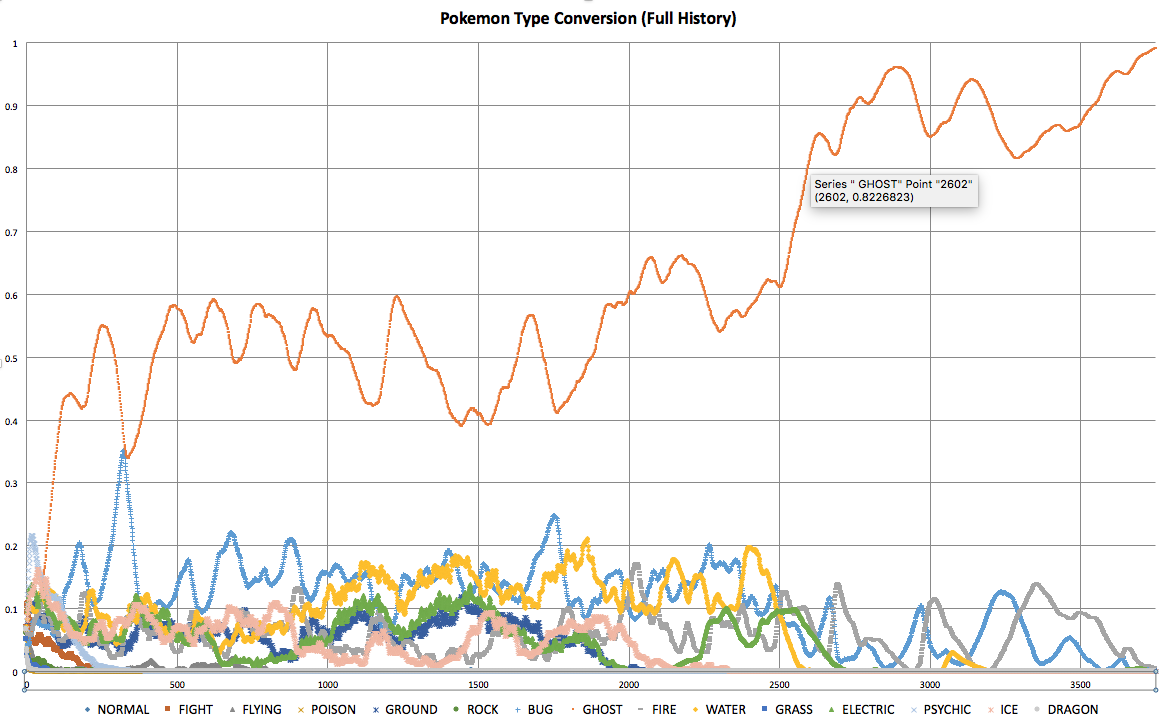	Run 4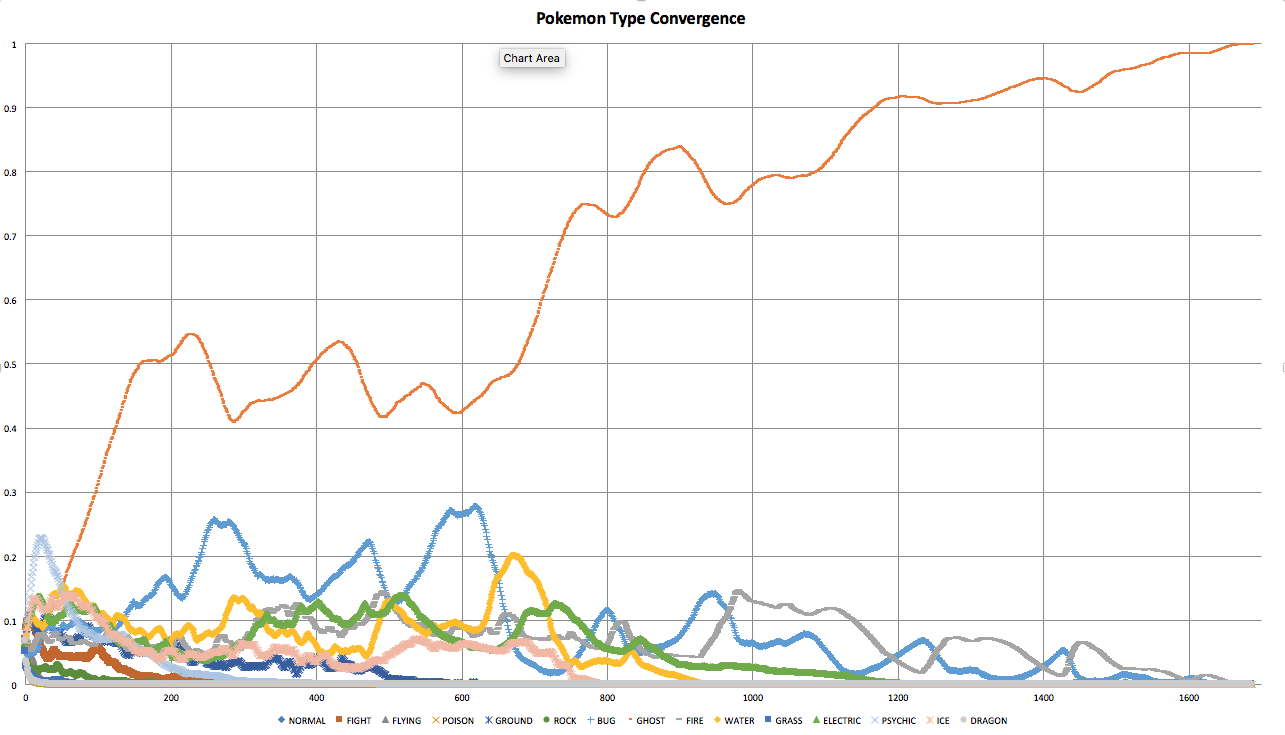
Run 2a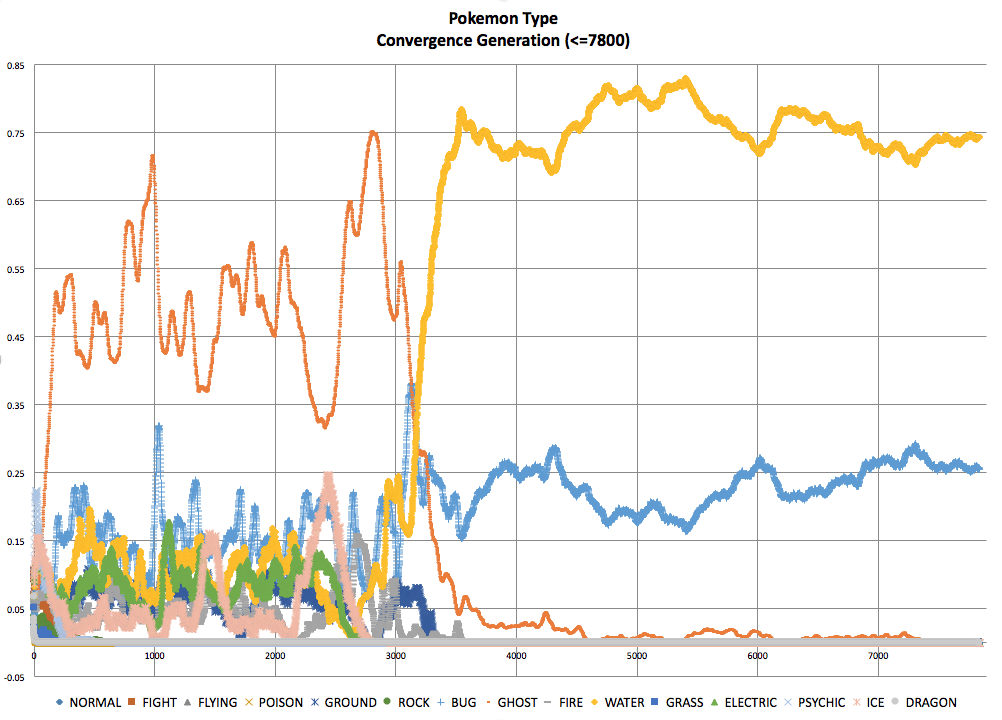	Run 2b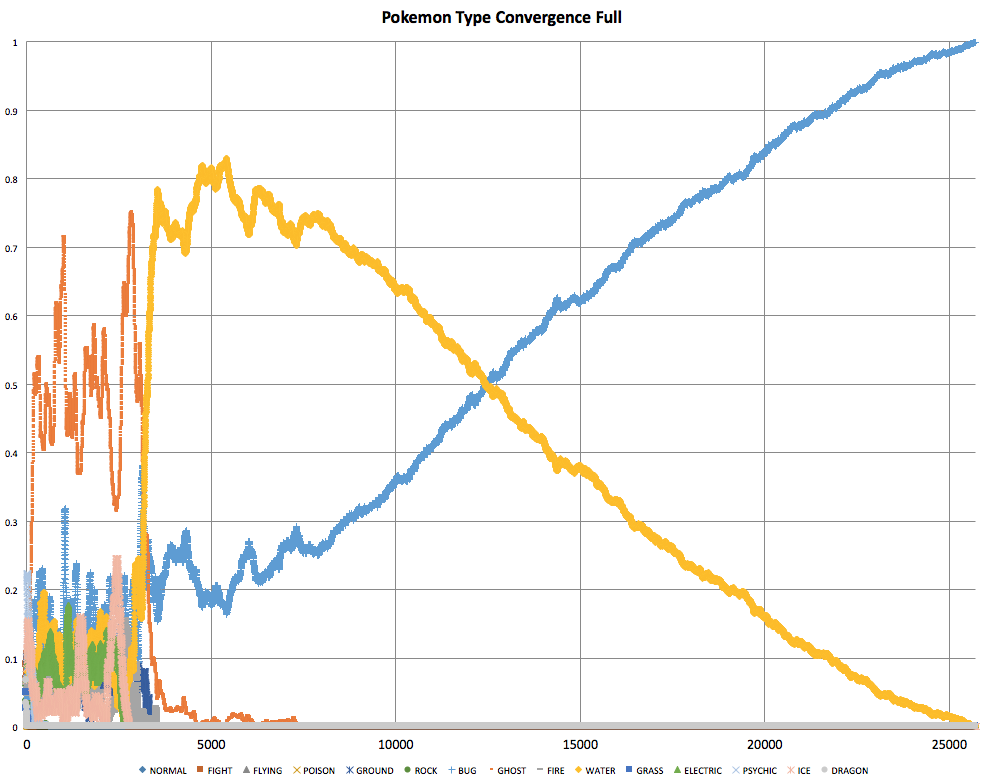

Conclusion

• Ghost wins the vast majority of the fights. This is largely due to it's immunities and relatively low overlap with other types. Specifically, nothing has an advantage over Ghost, except other Ghost.
• Most simulations come down between Bug and Ghost. I did not expect Bug to be so strong.
• Sometimes Ghost and Normal press against each other (unmoving as they are immune to each other). This grid-lock typically ends when one side gets cannibalized from the inside by another type.
• Many of the end games end with Water, Lightning, Ground fighting very aggressively back and forth while Bug and Ghost fight a slower battle in and around the three.
• It seems that Bug due to number and position is almost always prime to beat Ghost. However, Bug is regularly being wiped out in mass by other types. Though Bug seems to recover in most places. I saw one simulation where Bug would destroy much of Ghost, and then Fire would instantly devour 99% of Bug Pokemon. Then Ghost would devour most of Fire Pokemon. This would then give Bug a chance to rebound, until Fire took it out again.
• Turning on and off "friendly fire" seemed to slow, but not stop Bug's progression. Though the simulations do seem to drag out more. (Friendly fire == attacking same typed Pokemon)

Thanks for reading!